pearu.github.io

CSR random sampling

This blog post is inspired by PyTorch issue 59379 that seeks for a better sampling method for generating random CSR tensors to be used for testing PyTorch CSR tensor support. In the following, we’ll review the currently used method, then define what is a good sampling method for testing purposes, and finally, propose a new sampling method for generating CSR tensors to be used for testing algorithms using CSR tensors as inputs. It is important to note that the proposed sampling method is not meant to have specific statistical properties that would be useful for generating random CSR tensors for other purposes than testing CSR based algorithms.

Current state

At the time of writting this, PyTorch implements the following algorithm for sampling CSR tensors (here given a slightly modified version for clarity):

# Inputs: n_rows, n_cols, nnz
# Outputs: crow_indices, col_indices, values
nnz_per_row = nnz // n_rows
crow_indices = torch.zeros(n_rows + 1)
if nnz_per_row > 0:
    crow_indices[1:] = nnz_per_row
else:
    crow_indices[1:nnz + 1] = 1
crow_indices.cumsum_(dim=0)
actual_nnz = crow_indices[-1]
col_indices = torch.randint(0, n_cols, size=[actual_nnz])
values = make_tensor([actual_nnz], low=-1, high=1)

Pros:

• the algorithm is very simple

Cons:

• while col_indices and values are random, crow_indices are not. This means that this sampler always produces CSR tensors with regular crow_indices with a specific structure while other possible structures are not generated for some fixed nnz value no matter how large is the number of samples.
• specifying nnz does not guarantee that the number of specified values in the generated sample will be equal to nnz (except when nnz is a integer multiple of n_rows)
• to achieve a low sparsity samples, one needs to specify larger nnz values than n_rows * n_cols. This means that there is a high chance that the current method produces crow_indices that invalidate the CSR invariant 5.3.

As an example, the following animation generates a series of samples with specified nnz varying from 0 to n_rows * c_cols.

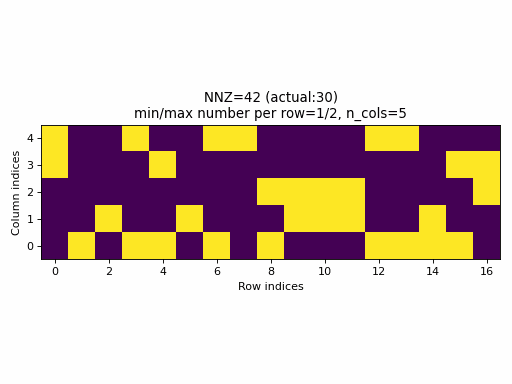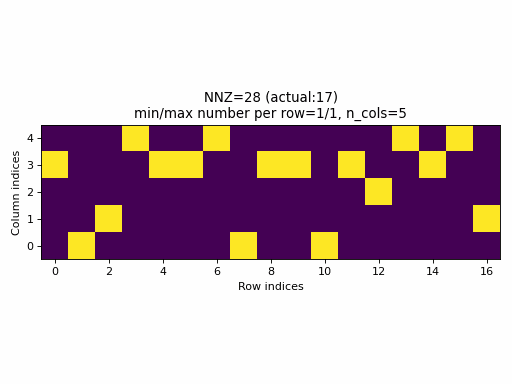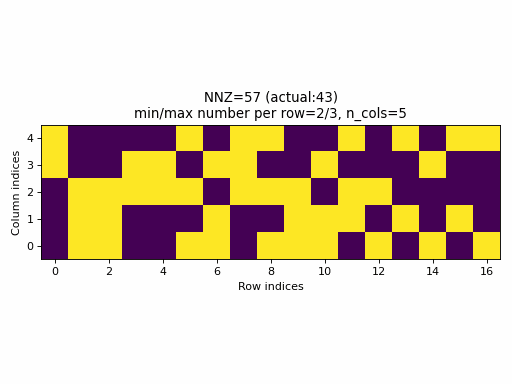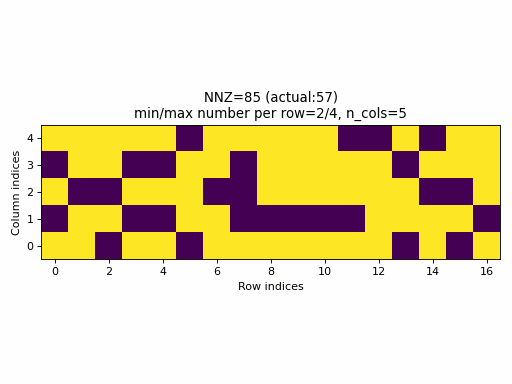
Observations:

• for a wide range of nnz values, rows with no entries or rows with all columns specified, are never generated (min/max number of columns per row is not equal to 0/n_cols),
• only for few specified values of nnz, it will be equal to the actual nnz value of the sample (observe the actual NNZ value),
• the distribution of specified elements looks uniform, however, this is not a good property, see the next section below.
• it is practically impossible to generate a CSR sample with a specified density. In fact, the set of possible densities is discrete, set((nnz // n_rows) / n_cols for nnz in range(0, n_rows, n_cols)), that appears to have size: n_cols.

Quality of random samples for testing

To test the correctness of some functionality in a software, using random samples with uniformly distributed specified elements is not always the optimal approach: edge cases such as existence of rows with no specified elements or with no unspecified elements, are practically never generated. However, often only the edge cases may reveal possible bugs in the corresponding algorithms/implementations.

So, the quality of random samples that are used for testing is not about the quality of the distribution of random placements of specified elements in the indices space of a sparse tensor. Instead, the quality is about maximally stressing the algorithms logic with a minimal effort. That is, a good sample has the following properties:

• it is small in order to minimize computation time when processing it in the algorithms,
• it will make all possible branches in the algorithm to be alive to maximize testing coverage,
• its structure is highly variable in order reveal any possible shortcomings of the algorithm,
• it must have some intrinsic randomness that will increase the variability of the structure even more when tests are run multiple times and/or from different environments,
• finally, its generation must be efficient.

In the case of generating samples of CSR tensors, the current quality of random samples is limited by the quality of crow_indices samples. So, in the following we aim at applying the properties of a good sample specifically to crow_indices and at the same time avoid the structural issues of the current sampler method, e.g., ensure that the actual nnz will be equal to the specified nnz parameter.

Sampling of crow_indices

To compute crow_indices, we are using the following model:

crow_indices = cumsum([0] + counts)

where counts is a list of integers with the following properties:

• len(counts) == n_rows
• counts[i] is the number of specified elements in the i-th row
• 0 <= counts.min() and counts.max() <= n_cols
• counts.sum() == nnz
• counts[-1] - counts[0] is as large as possible to maximize structural variability of row indices
• the distibution of different count values is as uniform as possible to obtain some balance between normal and the edge cases

In addition, we require that the computation of counts has complexity not greater than O(max(n_rows, n_cols)).

New algorithm

Clearly, there exists many solutions to counts that satisfy the above listed properties.

Here we propose a new algorithm that is based on computing the column counts per row from the following histogram:

      ^ count is the height of the histogram
      |
      |

        *   *   *   *   ###
       **  **  **  **+ o###
      *** *** *** ***+oo###
      @@@@@@@@@@@@@@@@@@###
      @@@@@@@@@@@@@@@@@@###      --> row indices

where different parts of the histogram are denoted as follows:

• <space> - no counts
• + - final correction
• o - an incomplete sawtooth
• * - a sequence of full sawteeth
• @ - lower rectangle
• # - right rectangle

Pseudo-code for computing the above histogram is as follows:

# Inputs: n_rows, n_cols, nnz
# Outputs: counts

counts = zeros(n_rows)

def N(n, m):
    # compute the total number of counts in the sequence of sawteeth
    M = (n_cols - m) * (n_cols - m + 1) // 2
    K = (n_rows - n) % (n_cols - m + 1)
    return M * ((n_rows - n) // (n_cols - m + 1)) + K * (K - 1) // 2

# Find n such that N(n, 0) == 0 or nnz - n * n_cols < max(N(n, 0), n_cols)
if n > 0:
    counts[-n:] = n_cols                        - this fills the region denoted by #

# Find m such that N(n, m) == 0 or nnz - n * n_cols - m * (n_rows - n) < max(N(n, m), n_rows - n)
if m > 0:
    counts[:n_rows - n] = m                     - this fills the region denoted by @

if N(n, m) == 0:  # no sawteeth
    counts[0] = nnz - n * n_cols - m * n_rows
else:
    q, r = divmod(nnz - n * n_cols - m * (n_rows - n), (n_cols - m) * (n_cols - m + 1) // 2)
    p = q * (n_cols - m + 1)
    # Find k such that k*(k+1)/2 <= r
    corr = r - k * (k + 1) // 2
    counts[:p] = arange(p) % (n_cols - m + 1)   - this fills the region denoted by *
    counts[p:p+k+1] += arange(k + 1)            - this fills the region denoted by o
    counts[p] += corr                           - this fills the region denoted by +

Notice that the filling of counts can use vectorized operations. To solve the equations N(n, m) == 0 for integers n and m, one can use the bisection algorithm.

For example, the following animation uses the above described construction of crow_indices for generating random CSR samples:

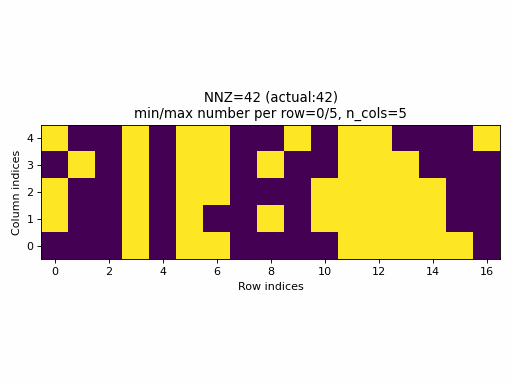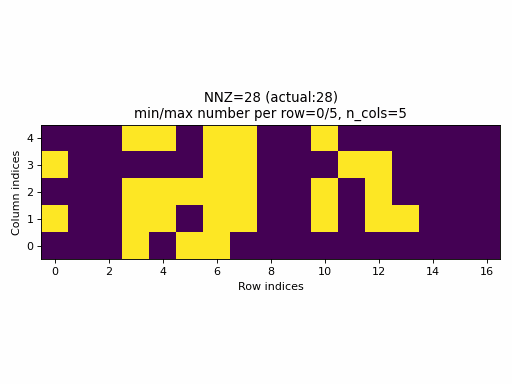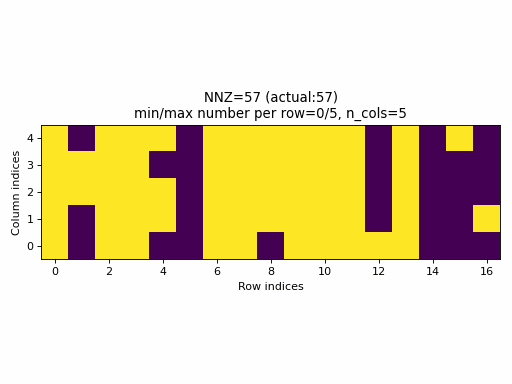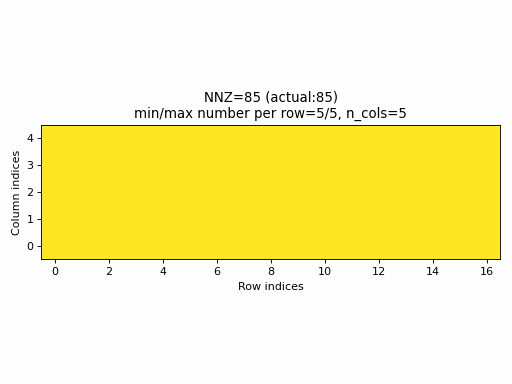
Observations:

• the nnz of the proposed CSR sample is always equal to the specified value of nnz, hence, the algorithm guarantees that a given density of the sparse tensor is always achievable by choosing nnz = int(density * n_rows * n_cols).
• the CSR sample contains rows with all possible number of columns: 0 to n_cols (unless the density is very low or very high when the property would not be achievable anyway).

More comparisons

Another way to compare the sampling methods is to disable randomization. Here follow the animations of the current and proposed samplings of CSR tensors:

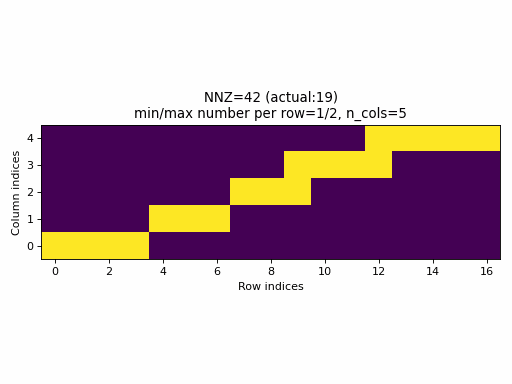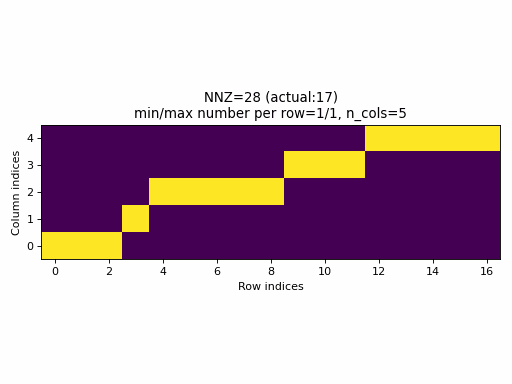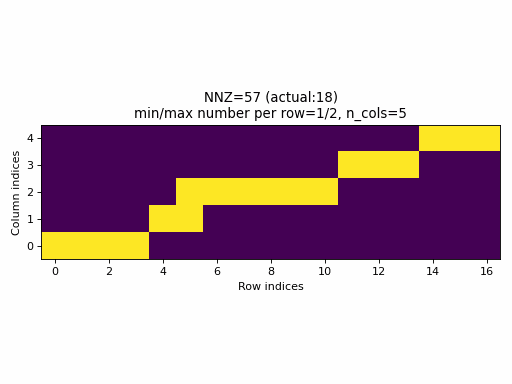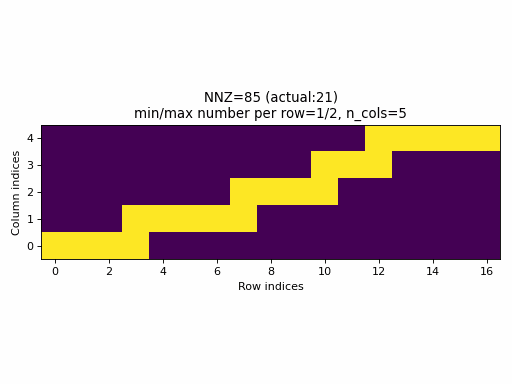
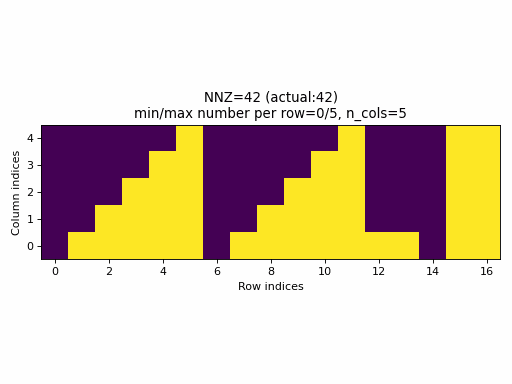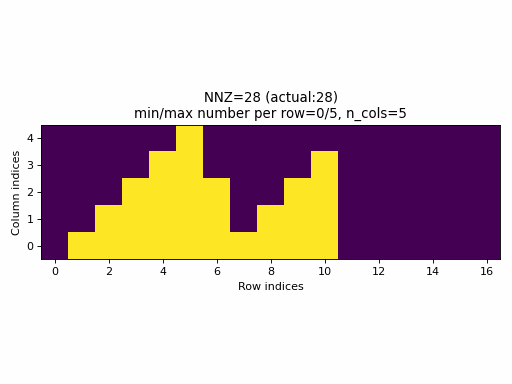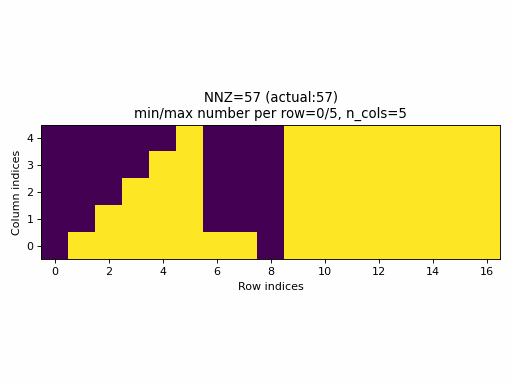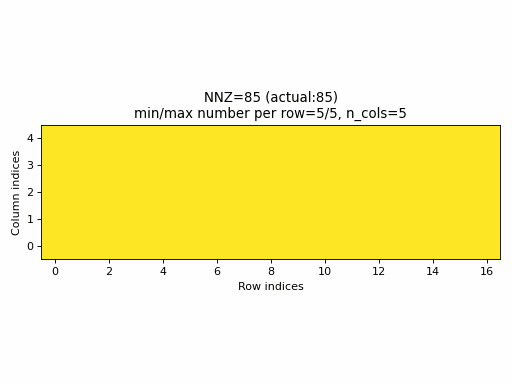
Observations:

• As seen above, the current sampling method in PyTorch produces the same indices structure for all nnz values. In fact, the sparsity of the CSR tensors is basically constant and it is impossible to generate low sparsity CSR samples with the current PyTorch sampling method.
• With the proposed sampling method the variability of indices structure is maximized for almost all nnz values. The sparsity of CSR samples varies within full range (from 0% to 100% of sparsity) when using the proposed sampling method.

Final notes

The animations produced in this blog post are generated using the Python script distribute_column_indices.py. The same script contains the prototype implementation of the proposed CSR sampling algorithm. For production implementation, see PyTorch PR 60283.

This site is open source. Improve this page.